栈和队列

技术探索
🗨️字数统计=1.4k字 ⏳阅读时长≈5分钟

一、栈

1. 栈的定义

  • 操作受限的线性表，先进后出 FILO（First In Last Out）

  • 一般设立栈顶指针初值为top=-1（栈空）

  • 从队头出队，从队头进队

    进栈：top ++;

    出栈：top –;

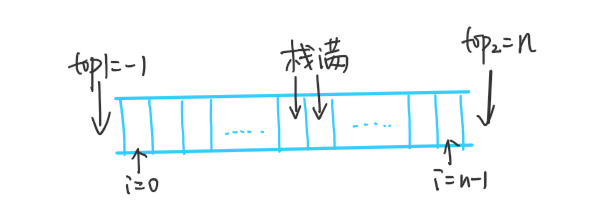
2. 共享栈：S[0 : n-1]

一般设初值为top1 = -1(栈空)，top2 = n(栈空)

当且仅当top2-top1 = 1时共享栈满（即两个栈顶指针相邻）

img

3. 出栈序列

若元素的进栈序列为ABCDE,运用栈操作，能否得到出栈序列BCAED和DBACE？

image-20200505110658107
  • BCAED 正确
  • DBACE 不可能：若 D 为首先出栈元素，已知 ABC 先于 D 入栈， C 不可能后于 AB 出栈

4. 实际应用举例

设计算法判断单链表（字符型data域)的全部n个字符是否中心对称。

ex: xyx, xyyx

思路：利用栈的先进后出的特点，将链表前一半元素依次进栈，然后将栈中元素出栈，与链表的后半元素依次进行比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int dc(LinkList L, int n){
  char s[n/2]; //字符栈，同数组实现栈的功能
  p = L->next;
  for(int i = 0; i < n/2; i++){ //链表前一半元素进栈
    s[i] = p->data;
    i++;
  }
  i--; //恢复最后的i值
if(n%2!=0) //若n为奇数，后移过中心结点
    p = p->next;
  while(p!=NULL && s[i]=p->data){ //检测是否中心对称
    i --; //i充当栈顶指针
    p = p->next;
  }
if(i = -1) //空栈
    return 1;
  else
    return 0;
}

5. 将中缀表达式转化为后缀表达式

核心思想 ：栈外字符加入栈内时，要保证栈外字符的优先级比栈内所有字符的优先级都要低，否则，弹出栈内优先级较高的字符，并加入后缀表达式。

步骤 ：

  • 遇到字母或数字直接入栈；

  • 遇到运算符时：

    • 若为’(‘, 直接入栈；
    • 若为’)’, 依次把栈中运算符加入后缀表达式，直到出现‘(’, 并从栈中将‘(’删除；
    • 若为其他运算符，根据优先级表依次弹出比当前处理的运算符优先级高的运算符，并将其加入后缀表达式，直到遇到一个比它优先级低的或遇到了一个’(‘为止。

运算符优先级表

操作符 # （ *，/ +，- ）
栈内优先级 0 1 5 3 6
栈外优先级 0 6 4 2 1

6. 栈在递归中的应用

ex：斐波拉契数列 0 1 1 2 3 5 …

1
2
3
4
5
6
7
8
int Fib(int n){
  if(n == 0)
    return 0;
  else if(n == 1)
    return 1;
  else c
    return Fib(n-1) + Fib(n-2);
}

递归必要的两个条件：

  • 递归表达式（递归体）
  • 递归出口（边界条件）

采用非递归方式重写递归程序时必须使用栈。该说法是错误的！

ex: 计算斐波拉契数列可用循环实现

函数调用时，系统要用栈保存必要的信息；递归次数过多容易造成栈溢出


二、队列

1. 队列定义

同样也是操作受限的线性表，先进先出FIFO，从队尾进队，从队头出队

队列分为：

  • 顺序队列
  • 循环队列
  • 链式队列
  • 双端队列

2. 顺序队列

  • 同样采用数组存储元素
  • 队头指针指向第一个元素
  • 队尾指针一般指向最后一个元素的下一个位置

进队：先送值到队尾，再将队尾指针+1

1
2
Q.data[Q.rear] = x;
rear ++;

出队：先取出队头元素，再将队头指针+1

1
2
x = Q.data[Q.front]
front ++;

顺序队列存在的问题 ：会导致上溢出；是一种 假溢出 ，在data数组中任然存在可以存放数组的位置

解决方法：

  • 建立一个足够大的存储空间以避免溢出，但这样做空间使用率低，浪费存储空间
  • 移动元素：每当出队一个元素，就将移动队列中所有的已有元素向队头移动一个位置
  • 循环队列：将队头和队尾看作是一个首尾相接的循环队列

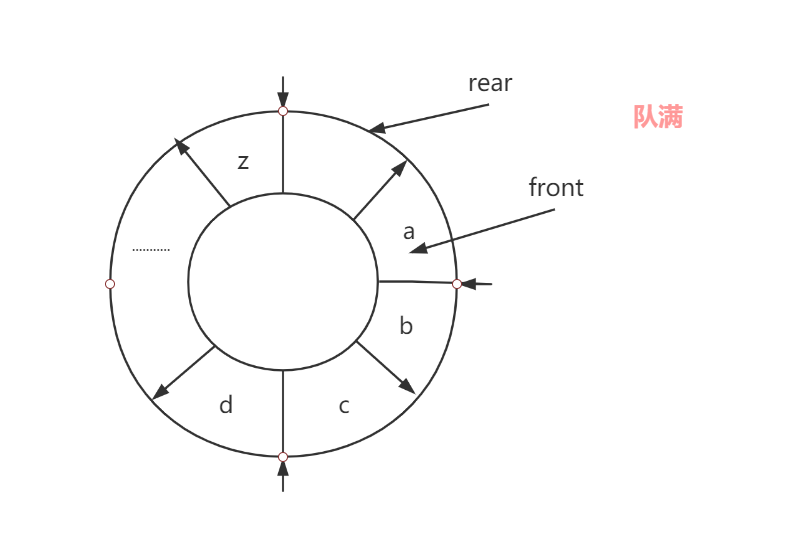
3. 循环队列

弥补顺序队列的缺点

  • 初始/队空：Q.front = Q.rear (队空条件）
  • 出队：Q.front = (Q.front+1) % maxsize (最大元素个数)
  • 进队：Q.rear = (Q.rear+1) % maxsize
  • 队列长度 = (Q.rear - Q.front + maxsize) % maxsize
  • 队满：( 牺牲一个单元来区分队空和队满 ）(Q.rear + 1) % maxsize = Q.front
img

4. 链式队列

实际就是一个同时带有头指针和尾指针的单链表

头指针指向队头结点，尾指针指向队尾结点（即单链表最后一个结点，与顺序存储有所不同）

适合于数据元素变动较大的情况，而且不存在队列满或者溢出的问题。

  • 队空： Q.rear == Q.front == NULL
  • 出队：（带头结点）
1
2
3
4
5
6
LinkNode *p = Q.front->next;
x = p->data;
Q.front->next = p->next; //插入头节点之后
if(Q.rear = p) //若原队列中只有一个结点，删除后变空，还需修改尾指针
    Q.rear = Q.front;
free(p);
  • 进队：（带头节点）
1
2
3
4
LinkNode *s = (LinkNode *) malloc (sizeof(LinkNode)); //创建新结点
s->data = x; s->next = NULL;
Q.rear->next = s; //插入到表尾
Q.rear = s;

5. 双端队列

允许两端都进行入队和出队操作的队列

  • 输出受限：有一端允许插入和删除；另一端只允许插入
  • 输入受限：有一端允许插入和删除；另一端只允许删除

6. 队列的应用

  • 层次遍历

  • 计算机系统中的应用

    • 解决主机与外部设备之间速度不匹配的问题（ex:打印机数据缓冲区中所存储的数据就是一个队列）
    • 解决由多用户引起的资源竞争问题（CPU将请求按时间先后排成队列）
分享到