树

技术探索
🗨️字数统计=2.5k字 ⏳阅读时长≈11分钟

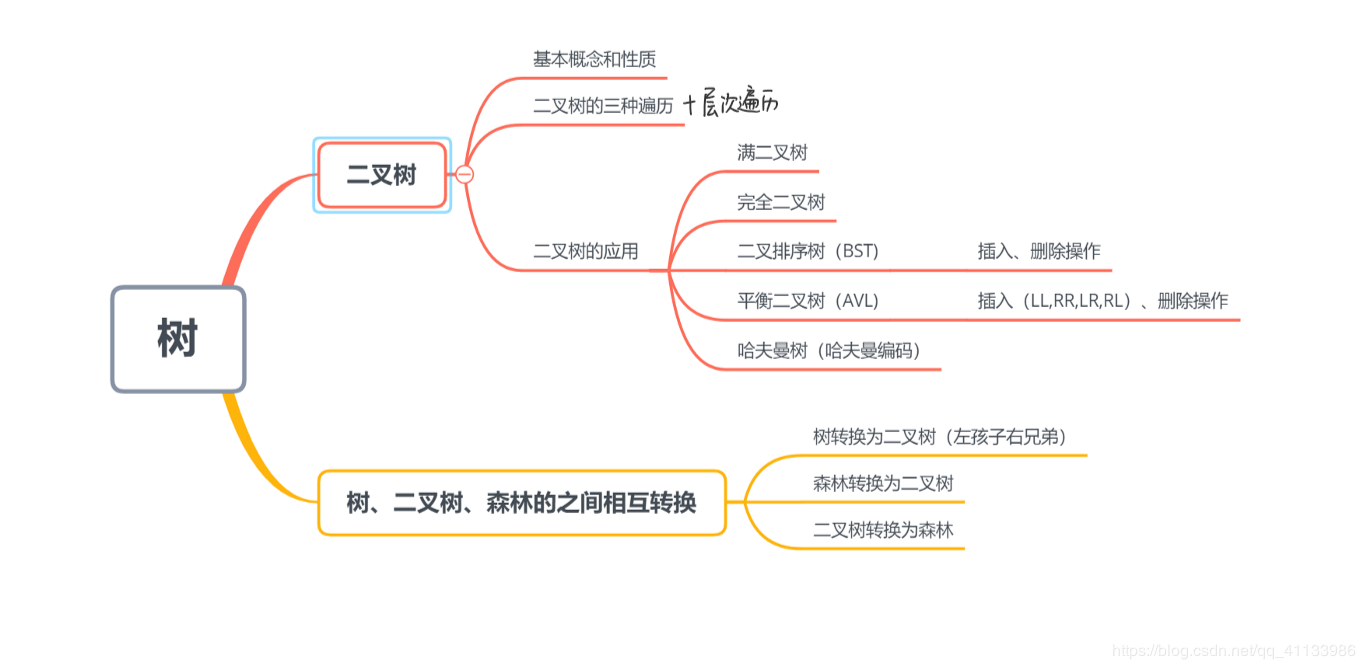
一、思维导图

img


二、基本概念和性质

  1. 结点数等于所有结点的度数(边数)加1 v = e+1；
  2. 对于一颗具有n个结点，度为4的树来说，树的最大高度为n-3；
    img
  3. 二叉树的性质：

  • n0 = n2 + 1； 叶子结点数数 = 度为2的结点+1

  • 高度为h的二叉树总共至多有 2的h次方 -1 个结点（满二叉树）
    第k层至多有 2的k-1次方 个结点；

  • 具有n个结点的完全二叉树的高度为 log2(n+1) 向上取整


三、二叉树的存储结构

顺序存储

顺序存储（数组）：空间利用率较低

链式存储

链式存储（链表）：左右孩子指针（含有n个结点的二叉链表中，含有n+1个空链域）

  • C
1
2
3
4
typedef struct BiTNode{
    int data;
    struct BiTNode* lchild,*rchild;
}BiTNode,*BiTree;
  • C++
1
2
3
4
5
6
7
template<class T>
struct BiTNode{
    T data;
    BiTNode<T> *lchild,*rchild;
    BiTNode():lchild(NULL),rchild(NULL){} //无参构造
    BiTNode(T x, BiTNode<T> *l = NULL, BiTNode<T> *r = NULL):data(x),lchild(l),rchild(r){} //带参构造
};

四、二叉树的三种遍历+层次遍历

以下代码给出三种遍历的递归和非递归实现，均为 c++ 实现

先中后遍历均借助栈实现，层次遍历借助队列实现

1. 先序遍历

  • 递归

    1
    2
    3
    4
    5
    public static void scan(BiTree b) {
        cout<<r->data;
        if(b->lchild != null) scan(b->lchild);
        if(b->rchild != null) scan(b->rchild);
    }

  • 非递归

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    //先序遍历非递归
    void InOrder(BiTree T){
        BiTree p = T;
        while(p || !is_empty(S)){
            if(p){
                visit(p->data);
                push(S,p);
                p=p->lchild;
            }
            else{
                pop(S,p);
                p = p->rchild
            }
        }
    }

2. 中序遍历

  • 递归

    1
    2
    3
    4
    5
    6
    7
    public static void scan(BiTree b) {
        if(b != null) {
            scan(b->lchild);
            cout<<r->data;
            scan(b->rchild);
        }
    }

  • 非递归

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    //中序遍历非递归
    void InOrder(BiTree T){
        BiTree p = T;
        while(p || !is_empty(S)){
            if(p){
                push(S,p);
                p=p->lchild;
            }
            else{
                pop(S,p);
                visit(p->data);
                p = p->rchild
            }
        }
    }

3. 后序遍历

  • 递归

    1
    2
    3
    4
    5
    6
    7
    public static void scan(BiTree b) {
        if(b != null) {
            scan(b->lchild);
            scan(b->rchild);
            cout<<r->data;
        }
    }

  • 非递归

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    //后序遍历非递归
    void PostOrder(BiTree T){
        InitStack(S);
        p = T;
        r = NULL; //最近访问过的结点
        while(p || !is_empty(S)){
            if(p){
                Push(S,p);
                p = p->lchild;
            }
            else{
                GetTop(S,p);
                //右孩子存在且未被访问过
                if(p->rchild && r!=p->rchild){
                    p = p->rchild;
                    Push(S,p);
                    p = p->lchild; //再走到最左
                }
                else{ //若既无左孩子也无右孩子，则弹出结点并访问
                    Pop(S,p); 
                    visit(p->data);
                    r = p; //置为最近访问结点
                    p = NULL; //p重置
                }
            }
        }
    }

4. 层次遍历

1
2
3
4
5
6
7
8
9
10
11
12
void LevelOrder(BiTree T){
    BiTNode p;
    EnQueue(Q,T);
    while(!isEmpty(Q)){
        DeQueue(p);
        visit(p);
        if(p->lchild!=NULL)
            EnQueue(Q,p->lchild);
        if(p->rchild!=NULL)
            EnQueue(Q,p->rchild);
    }
}

若已知以下三种序列组合，则可以唯一的确定一颗二叉树

  • 先序和中序序列（前序为进栈序列，中序为出栈序列）
  • 后序和中序序列
  • 层次和中序序列

  • 若非空二叉树先序序列和后序序列正好相反，则二叉树形态是什么?

    每层只有一个结点，高度=结点个数

  • 若非空二叉树先序序列和后序序列正好相同，则二叉树形态是什么？

    只有根节点


五、二叉树相关递归算法

1. 统计二叉树中度为2的结点个数

1
2
3
4
5
6
7
8
int Dnode(BiTree T){
    if(T==NULL)
        return 0;
    else if(T->lchild && T->rchild)
        return Dnode(T->lchild)+Dnode(T->rchild) + 1;
    else
        return Dnode(T->lchild)+Dnode(T->rchild);    
}

2. 统计二叉树中度为1的结点个数

1
2
3
4
5
6
7
8
int Lnode(BiTree T){
    if(T==NULL)
        return 0;
    else if(T->lchild==NULL&&T->rchild!=NULL || T->lchild!=NULL&&T->rchild==NULL)
        return Lnode(T->rchild)+Lnode(T->lchild)+1;
    else
        return Lnode(T->rchild) + Lnode(T->lchild);
}

3. 统计二叉树中度为0的结点个数(叶子)

1
2
3
4
5
6
7
8
int Leaves(BiTree T){
    if(T==NULL)
        return 0;
    else if(T->lchild==NULL && T->rchild==NULL)
        return 1;
    else 
        return Leaves(T->rchild) + Leaves(T->lchild);
}

4. 统计二叉树的高度

1
2
3
4
5
6
7
8
9
10
11
int Height(BiTree T){
    if(T==NULL)
        return 0;
    else if(!T->lchild && !T->rchild)
        return 1;
    else{
        int hl = Height(T->lchild);
        int hr = Height(T->rchild);
        return (hl>hr?hl:hr) + 1;
    }
}

5. 统计二叉树的宽度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//先序遍历，每递归一次就深入一层
int count[100]; //记录每层的宽度
int Width(BiTree T,int k){ //K表示第几层
    int max = -1;  //最大宽度
    if(T==NULL)
        return 0;
    count[k] ++; //第k层宽度++
    if(max<count[k])
        max = count[k];
    else{
        Width(T->lchild,k+1);
        Width(T->rchild,k+1);
    }
}

6. 计算指定结点*p所在层次

1
2
3
4
5
6
7
8
9
10
11
12
13
int Level(BiTree T, BiTNode *p, int level){
    if(T==NULL)
        return 0;
    else if(T->data == p->data)
        return level;
    else{
        int l = Level(T->lchild,p,level+1);
        if(l!=0)
            return l;
        else
            return Level(T->rchild,p,level+1);
    }
}

7. 交换二叉树中每个结点的两个子女

1
2
3
4
5
6
7
8
9
10
//先交换左右孩子的左右子树，再交换左右孩子
void swap(BiTree T){
    if(T){
        swap(T->lchild);
        swap(T->rchild);
        int temp = T->lchild;
        T->lchild = T->rchild;
        T->rchild = temp;
    }
}

六、二叉排序树BST / 二叉查找树

1. 定义

二叉排序树又称二叉查找树，它或者是一颗空树，或者满足一下性质的二叉树：

  • 若左子树不空，则左子树上所有结点的值均小于根节点的值；
  • 若右子树不空，则右子树上所有结点的值均大于根节点的值；
  • 左右子树也分别是二叉排序树。

递归的数据结构，左<根<右 ，中序遍历为递增序列

2. 插入和删除操作

  • 插入

    插入的结点一定是某个叶结点

  • 删除
    • 被删除结点时叶子结点，直接删除；
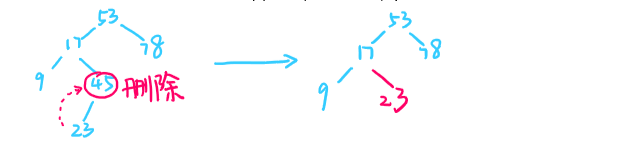
    • 被删除结点z只有一棵左子树或者右子树，则删除z,令z的子树成为z父结点的子树
      img
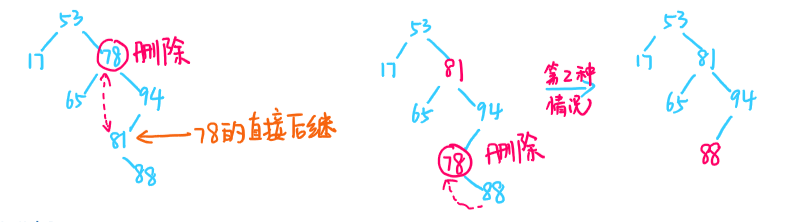
    • 被删除结点z有两棵子树，则交换z的 直接后继（中序遍历） 和z的位置，转换为第二种情况删除z
      img
  • 查找效率分析
    • 最好情况：平衡二叉树 O(log2n)
      img
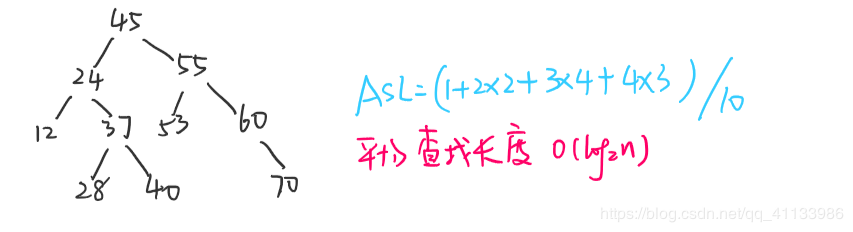
    • 最坏情况：输入序列有序 O(n)
      img

3. 二叉排序树的判定

思路：二叉排序树的中序遍历序列一定为递增序列

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
//利用中序遍历为递增
bool isBST(BiTree T){
    if(T==NULL)
        return true;
    else{
        bool bl = isBST(T->lchild);
        if(bl==false || pre>T->data)
            return false;
        pre = T->data;
        bool br = isBST(T->rchild);
        return br;
    }
}

七、平衡二叉树AVL

1. 定义

为避免树的高度增长过快，降低二叉排序树的性能，

规定插入和删除时 任意结点的左右子树高度差的绝对值不超过1 。

平衡二叉树是特殊的二叉排序树

2. 插入操作（每次调整对象都是最小不平衡子树）

  1. LL右单旋：（在结点A的左孩子的左子树插入新结点导致A失衡）
    img
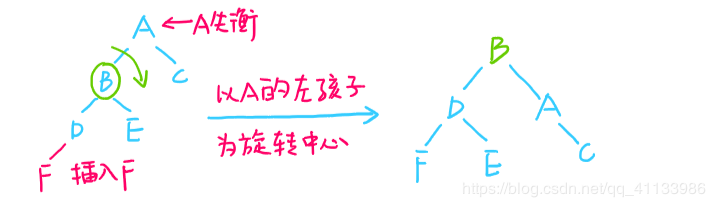
  2. RR左单旋：（在结点A的右孩子的右子树插入新结点导致A失衡）
    img
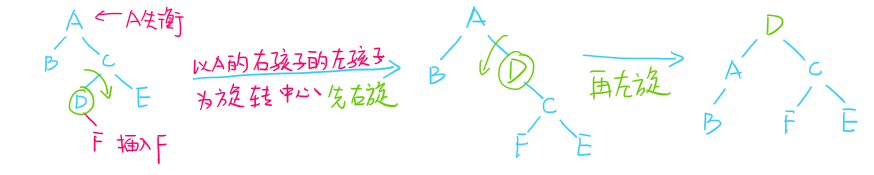
  3. LR左右双旋：（在结点A的左孩子的右子树插入新结点导致A失衡）
    img
  4. RL右左双旋：（在结点A的右孩子的左子树插入新结点导致A失衡）
    img

3. 平衡二叉树的判定

思路：平衡二叉树的每一个结点都是平衡的，利用后序遍历按照左右根的次序依次判断是否平衡二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int isAVL(BiTree T,int &h,int &balance){
    int bl,br,hl,hr; //左右子树的高度和平衡性
    if(T==NULL){
        balance = 1;
        h = 0;
    }
    else if(!T->lchild && !T->rchild){ //左右孩子均不存在
        balance = 1;
        h = 1;
    }
    else{
        isAVL(T->lchild,hl,bl); //判定左子树
        isAVL(T->rchild,hr,br); //判定右子树
        h = hl>hr?hl:hr;
        if(bl&&br && abs(hl-hr)<2) //若左右子树均平衡且高度差小于等于1
            balance = 1;
        else
            balance = 0;
    }
}

4. 完全二叉树的判定

思路： 完全二叉树的结点编码是连续的，根据层次遍历，把所有结点依次入队，包括空结点，若空结点之后还有非空结点，就不是完全二叉树

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool isComplete(BiTree T){
    if(!T)
        return true;
    InitQueue(Q);
    BiTNode *p = T;
    EnQueue(Q,T);
    while(!isEmpty(Q)){
        DeQueue(Q,p);
        if(p){
            EnQueue(Q,p->lchild);
            EnQueue(Q,p->rchild);
        }
        else{
            while(!isEmpty(Q)){
                DeQueue(Q,p);
                if(p)
                    return false;
            }
        }
    }
    return true;
}

八、哈夫曼树（最优二叉树）和哈夫曼编码

1. 定义

给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman tree)

带权路径长度：结点到根结点之间的路径长度与该结点上权的乘积

2. 构造方法

每次选取两棵根结点权值最小的树作为新结点的左右子树

img

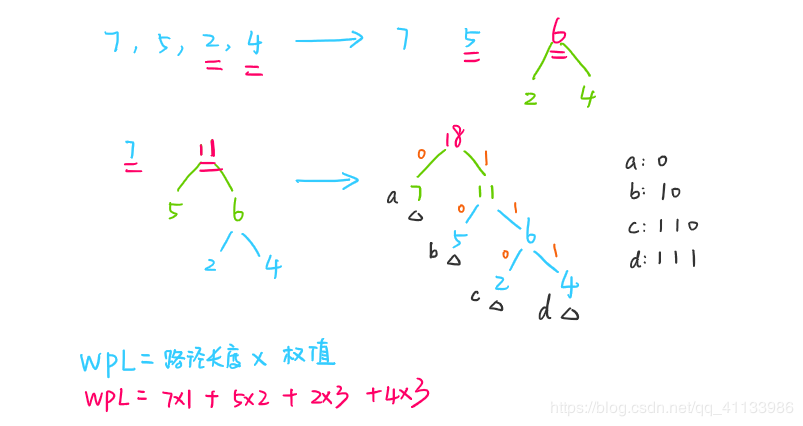
3. 哈夫曼编码

前缀编码：没有一个编码是另一个编码的前缀，比如：01 011 010 就不是前缀编码，因为01是011的前缀，根据01不能唯一确定用哪个编码。

哈夫曼编码就是长度最短的前缀编码，减少编码的长度。


九、树、森林、二叉树的转换

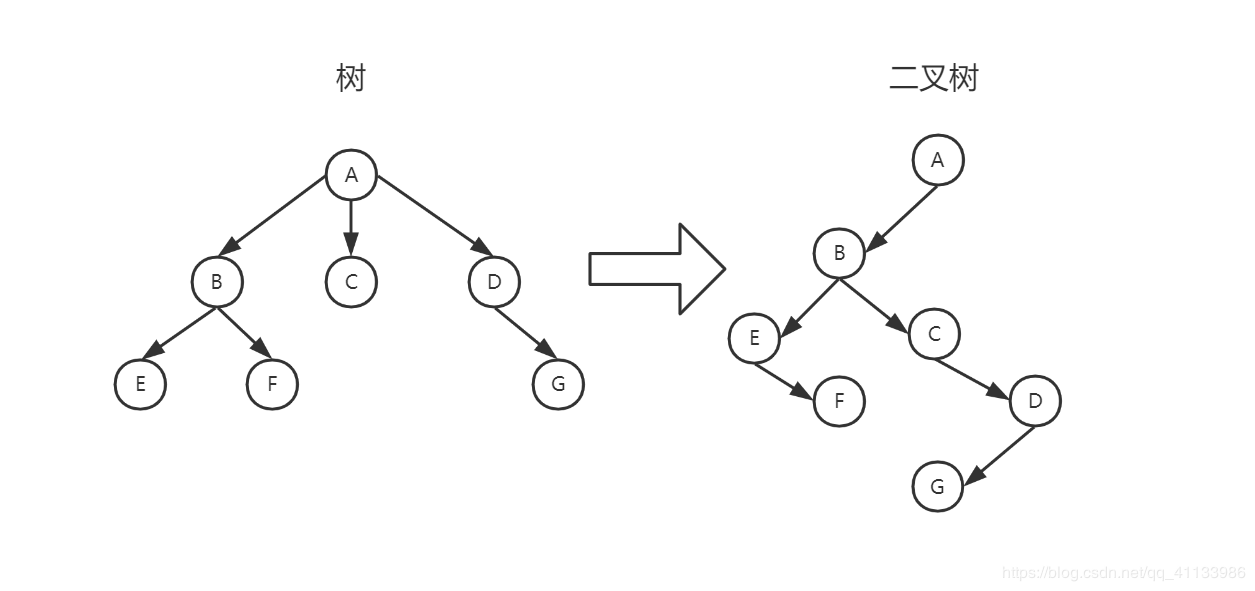
1. 树转化为二叉树

二叉树中遵循 左孩子右兄弟 的原则

img

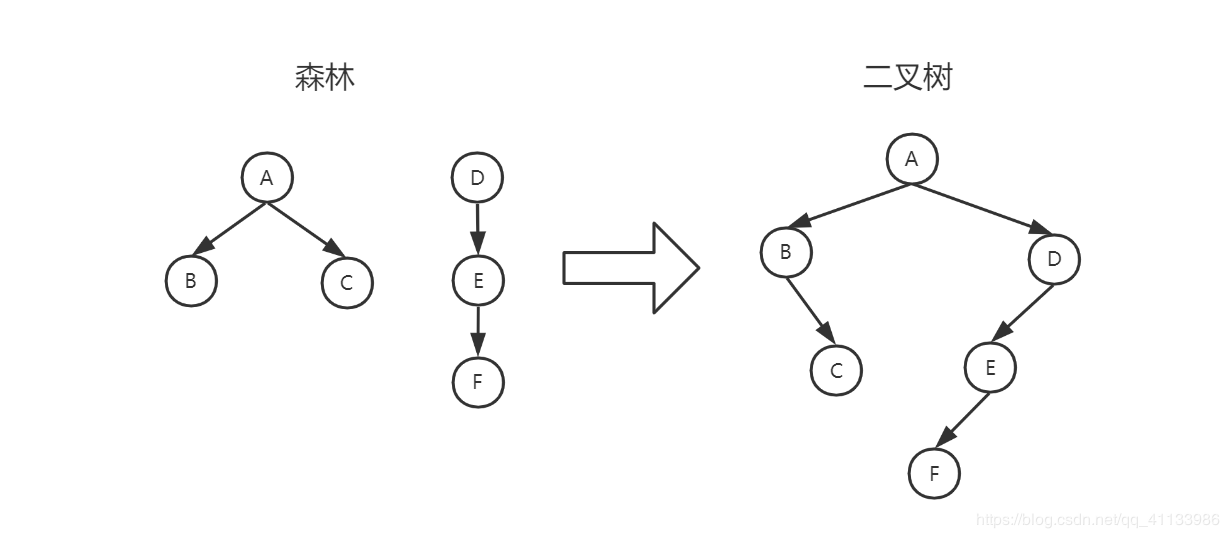
2. 森林转化为二叉树

  • 将第一棵树的根作为转换后的二叉树的根；
  • 将第一棵左子树作为转换后二叉树根的左子树；
  • 将第二棵树作为转化后二叉树的右子树……….

img

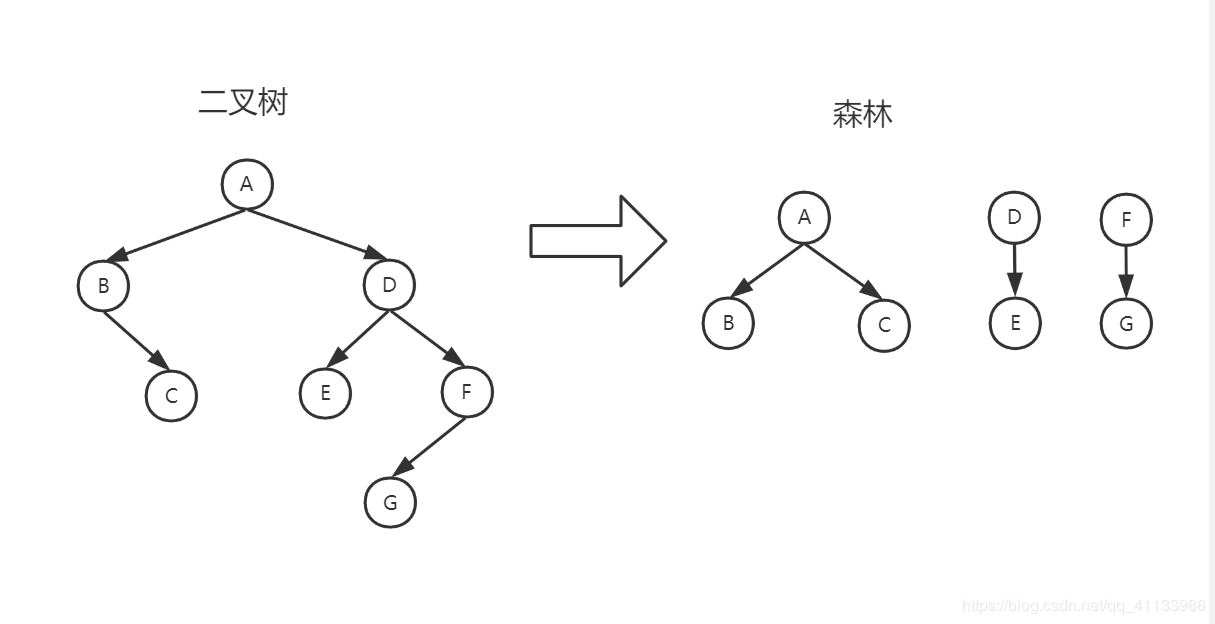
3. 二叉树转化为森林

  • 二叉树的根及其左子树作为第一棵树；
  • 右子树作为第二棵树；
  • 直到产生一棵没有右子树的二叉树为止
    img
分享到