查找

技术探索
🗨️字数统计=1.9k字 ⏳阅读时长≈7分钟

思维导图

img


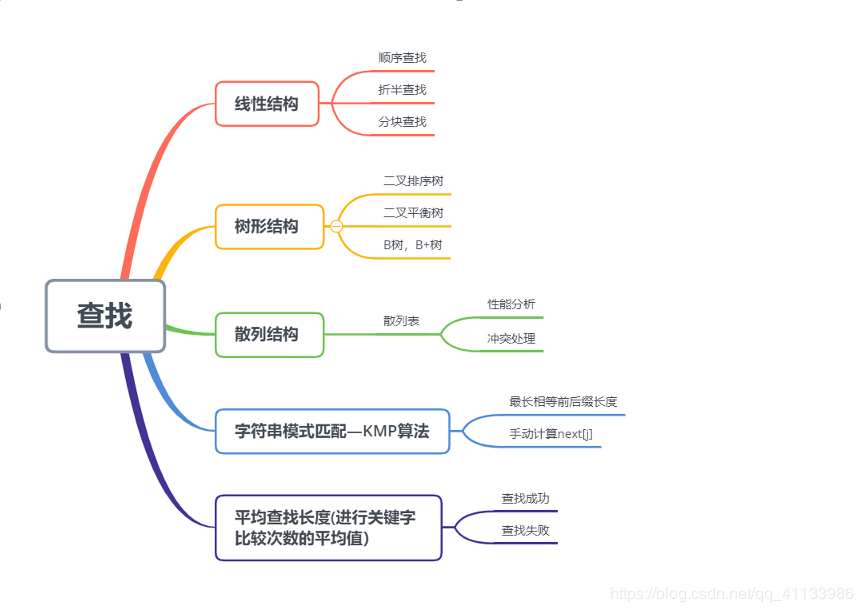
一、线性结构

1. 顺序查找（线性查找）O(n)

主要用于在线性表上进行查找

1
2
3
4
5
6
7
8
int Search_Seq(int *a,int x){
    //a[0]作哨兵，使得循环不必判断数组是否越界
    //因为满足i==0时，循环一定会跳出
    a[0] = x; 
    int i; 
    for(i = 10;a[i]!=x;i--);
    return i;
}

注：对于顺序查找，不管线性表是有序的还是无序的，成功查找第一个元素的比较次数为1，成功查找第二个元素的比较次数为2，依次类推，每个元素查找成功的比较次数只与其位置有关，与是否有序无关。

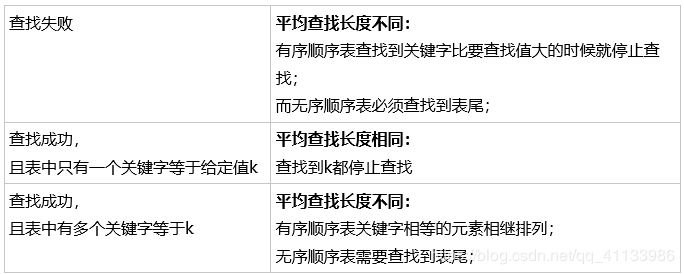
对有n个元素的有序顺序表和无序顺序表进行顺序查找，讨论平均查找长度

img

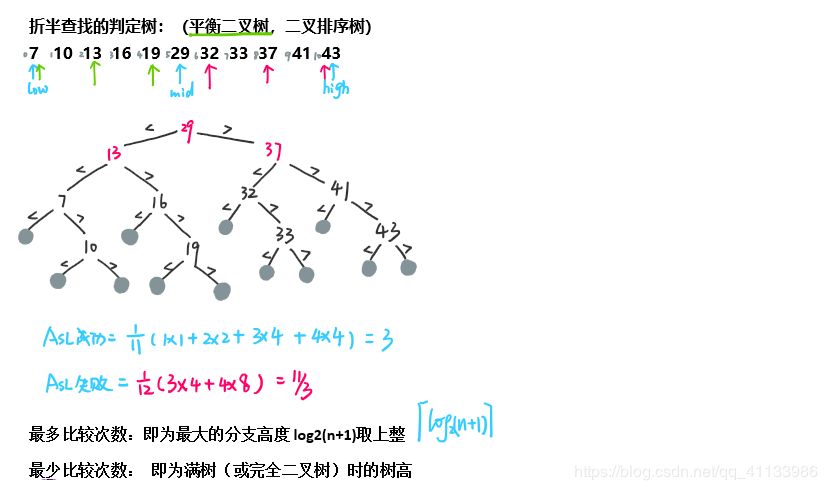
2. 折半查找(仅适用于有序的顺序表) O(log2n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int Binary_Search(int *a,int x){
    int low = 0, high = 10,mid;
    while(low<=high){
        mid = (low+high)/2;
        cout << a[low] << setw(5) << a[mid] << setw(5) << a[high] << endl;
        if(a[mid]==x)
            return mid;
        else if(a[mid]<x)
            low = mid+1;
        else
            high = mid-1;
    }
    return -1; //若查找成功不会走到这一步
}

img

img

3. 分块查找（索引顺序查找）

块中元素可无序，块间元素须有序

img


二、树形结构

1. 二叉排序树

详见 第三章节 - 树

2. 平衡二叉树

详见 第三章节 - 树

3. B / B+ 树

B/B+树一种平衡的多路查找树，一般被用在文件系统（我们常说的B树其实是叫 B- 树）

B 树 M阶 B+ 树 M阶
① 关键字个数 + 1 = 子树个数 ① 关键字个数 = 子树个数
② 根节点至少2棵子树（1个关键字），至多M棵子树（M-1个关键字） ② 根节点至少2棵子树（2个关键字），至多M棵子树（M个关键字）
③ 除根节点的分支结点至少 M/2 取上整 棵子树（至少 M/2 取上整 - 1 个关键字），至多 M 棵子树（至多 M - 1个关键字） ③ 除根节点的分支结点至少 M/2 取上整 棵子树至少 M/2 取上整 -个关键字），至多 M 棵子树至多 M 个关键字）
④ B 树的叶节点不带任何信息，所有的信息（key，value）都存在分支结点中 ④ B+树叶子结点携带所有结点的全部信息（key，value），且按照大小顺序通过指针链接起来，分支结点仅携带索引信息（key）起索引作用。所以B+ 树的查找更稳定，因为每次都是从根节点到叶节点的查找路径

下图为 B+ 树

B树的插入删除操作

插入：

  • 插入后该结点关键字个数小于等于m-1，直接插入
  • 插入后该结点关键字个数大与m-1，以该结点的中间元素为轴进行结点分裂，并将该结点的中间元素上移到其父结点，相应的父结点要增加新分支，即分裂的结点

img

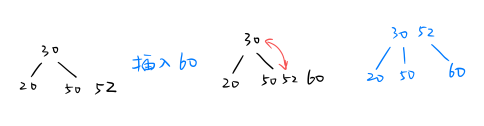
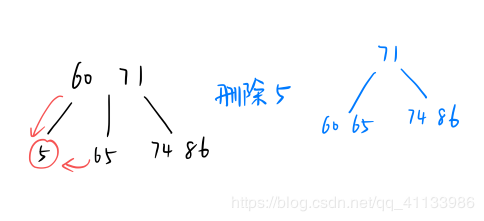
删除（叶节点）：以3阶为例

  • 删除该关键字后所在结点的关键字个数 > [m/2]取上整 - 1, 直接删除关键字
  • 删除该关键字后所在结点的关键字个数 < [m/2]取上整 - 1 且与其相邻的左（右）兄弟结点够借 ， 父子换位法（兄弟的第一个元素上移到父结点，父结点的最后一个元素下移到要删除的关键字所在的结点。—— 兄弟够借，父子换位
    img
  • 删除该关键字后所在结点的关键字个数 < [m/2]取上整 - 1 且与其相邻的左（右）兄弟结点不够借 ， 则将关键字删除后，将父结点第一个元素下移至要删除元素所在结点处 并与其兄弟结点合并 —— 兄弟不够借，父子合并
    img

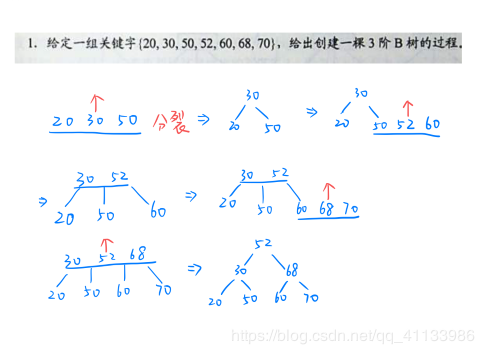
B树的建立过程举例：

img

4. 红黑树

① 为什么需要红黑树

对于二叉搜索树，如果插入的数据是随机的，那么它就是接近平衡的二叉树，平衡的二叉树，它的操作效率（查询，插入，删除）效率较高，时间复杂度是O（logN）。

但是可能会出现一种极端的情况，那就是插入的数据是有序的（递增或者递减），那么所有的节点都会在根节点的右侧或左侧，此时，二叉搜索树就变为了一个链表，它的操作效率就降低了，时间复杂度为O(N)，所以可以认为二叉搜索树的时间复杂度介于O（logN）和O(N)之间，视情况而定。

那么为了应对这种极端情况，红黑树应运而生，它是具备了某些特性的二叉搜索树，能解决非平衡树问题，红黑树是一种接近平衡的二叉树。

② 红黑树的特征

首先，红黑树是一个二叉搜索 / 二叉排序树，它同时满足以下特性：

  • 每个节点非黑即红

  • 根节点是黑色

  • 如果节点是红色的，那么它的子节点必须是黑色的（反之，不一定需要成立）

  • 从根节点到叶节点或空子节点的每条路径，都包含相同数目的黑色结点

③ 红黑树的效率

红黑树的查找，插入和删除操作，时间复杂度都是O(logN)。

查找操作时，它和普通的相对平衡的二叉搜索树的效率相同，都是通过相同的方式来查找的，没有用到红黑树特有的特性。

但，如果插入的时候是有序数据，那么红黑树的查询效率就比二叉搜索树要高了，因为此时二叉搜索树不是平衡树，它的时间复杂度O(N)。

插入和删除操作时，由于红黑树的每次操作平均要旋转一次和变换颜色，所以它比普通的二叉搜索树效率要低一点，不过时间复杂度仍然是O(logN)。

总之，红黑树的优点就是对有序数据的查询操作不会慢到O(logN)的时间复杂度。

④ 红黑树的操作

👉 红黑树详解


三、散列结构

散列表

img

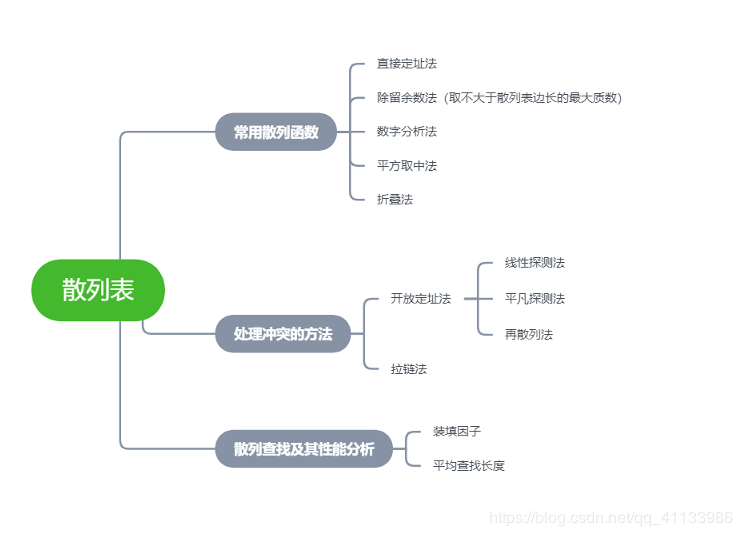
1. 散列表的定义

散列（哈希）表： 根据关键码值(Key value)而直接进行访问的数据结构 。根据给定的关键字通过散列函数来计算出关键字在表中的地址，以加快查找的速度。

2. 散列函数的构造方法

  1. 直接定址法
    H(key) = a*key + b
  2. 除留取余法
    H(key) = key%p (p为不大于m的最大质数)

3. 散列（哈希）冲突

冲突：指的是多个关键字映射同一个地址的情况。

4. 处理冲突的方法

1.开放定址法

  • 线性探测法（常用，会产生堆积问题）

    冲突发生时顺序查找下一个位置

  • 平方探测法

  • 再散列法

2.拉链法（所有的同义词都存储在一个线性链表中）

img

5. 性能分析

平均查找长度仅依赖于装填因子，越满发生冲突的可能性越大。

  • ASL成功 （除以 元素的总个数）
  • ASL失败 （除以 P 或 mod后面的数）

四、字符串模式匹配

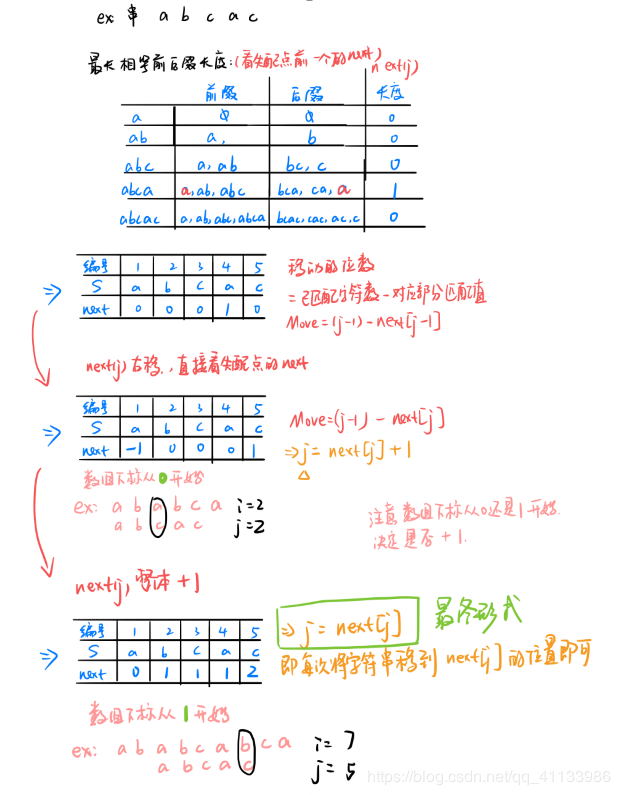
KMP 算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int Index_KMP(string s,string T,int next[],int pos){
    int i = pos,j = 1; //i代表母表，j代表字表
    while(i<=s.length && j<T.length){
        if(j==0 || s[j]==T[i]){
            i++;
            j++;
        }
        else
            j = next[j];
    }
    if(j>T.length) //匹配成功
        return i-T.length;
    else
        return 0;
}

next 数组算法如下：

img

分享到